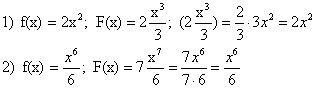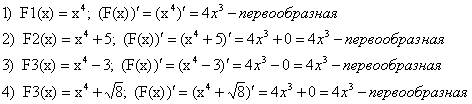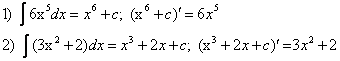Функцию восстанавливаемую по её производной называют первообразной.
Если выполняется равенство  , то функция , то функция  является первообразной для является первообразной для 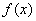
Найти первообразную: 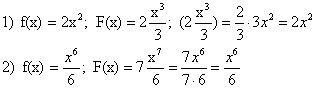
Проверить какая из следующих функций является первообразной для функции 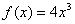
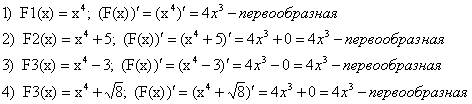
Вывод: Все эти четыре функции являются первообразными для одной в этом состоит неоднозначность вычисления первообразной.
Определение: Совокупность всех первообразных 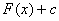 , где с – любое число, называется неопределённым интегралом и обозначается , где с – любое число, называется неопределённым интегралом и обозначается 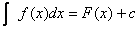 , где , где  называется подъинтегральным выражением, называется подъинтегральным выражением,  - подъинтегральной функцией, а x – переменное интегрирование. Например: - подъинтегральной функцией, а x – переменное интегрирование. Например: 
Слово интеграл происходит от латинского Integer и означает восстановленный.
Чтобы проверить правильно ли вычислен интеграл необходимо найти производную полученной функции.
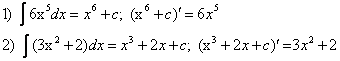
Основные свойства неопределённого интеграла:
- Производная неопределённого интеграла равна подъинтегральной функции:

- Постоянные множитель подъинтегральной функции можно вынести за знак интеграла (также относится это свойство к подъинтегральному выражению)
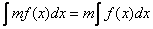
- Интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интеграла этих функций
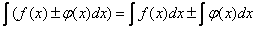
Представить интеграл как алгебраическую сумму: 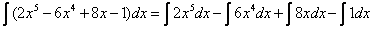
Неопределённый интеграл
Дифференцирование – это действие, с помощью которого по данной функции находится её производная или дифференциал. Например, если 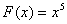 , то , то 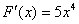 , , 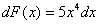
Теорема: если  - первообразная для - первообразная для  на некотором промежутке, то и функция на некотором промежутке, то и функция  , где с –любая постоянная, также является первообразной для функции , где с –любая постоянная, также является первообразной для функции  на этом промежутке. на этом промежутке.
Непосредственное интегрирование. Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путём тождественных преобразований подъинтегральной функции и применения свойств неопределённого интеграла приводится к одному или нескольким табличным интегралам. |